Looking for a tutorial on How To Type Subscript Characters? This practical video explains exactly how it's done, and will help you get good at computer basic. About 7 months ago I decided to try out WolframAlpha Pro. Paid for 6 months. The second day I was going to use the pro feature to see step-by-step solutions I was unable to do so as the website didn't acknowledge that I was logged in - even though I was.

Using the Fast Query Recognizer API
Sample Query
Now that you have an AppID, you can make your first query. The base URL for queries is:
Every query requires three pieces of information—an AppID, a mode and an input value—in order to be processed correctly. The appid parameter tells your query which AppID to use:
The Fast Query Recognizer has two distinct modes, 'Default' and 'Voice', explained below. For the purposes of this sample query, we'll use the 'Default' mode:
Next, use the i parameter to specify the URL-encoded input for your query. For instance, here is a query for 'France':
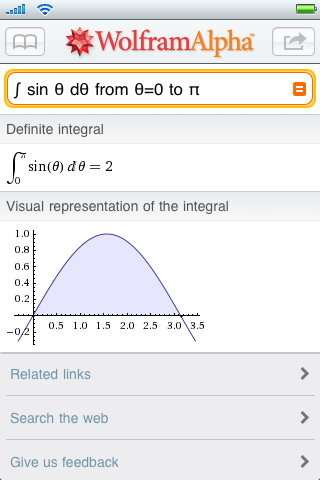
When executed with a valid AppID, this URL will return an image with informational elements relating to the input:
URL Parameters and Options
You can add URL-encoded parameters to customize the behavior and output of the Fast Query Recognizer.
mode
The Fast Query Recognizer is available in two different modes, each of which is configured to accept certain types of inputs. 'Default' mode is designed to recognize any query for which Wolfram|Alpha returns a relevant result, with the goal of placing as many answers as possible into results. Some specific types of queries (e.g. phone numbers, IP addresses, product codes) are explicitly filtered, and only inputs with unambiguous linguistics are accepted (e.g. 'boston employment' is not accepted, but 'boston employment rate' is). This tuning up for ambiguity is an ongoing improvement.
The 'Voice' mode of the Fast Query Recognizer is optimized for spoken input. It is generally less restrictive than the 'Default' mode, meaning that more variation of the input will be accepted.
output
How To Type Subscript On Mac For Wolfram Alpha X
Results from the Fast Query Recognizer are available in both XML (default) and JSON formats using the output parameter. Here is the JSON version of the sample query and result from above:
How To Type Subscript Mac
Output Parameters
The following is an explanation of the output parameters given in XML and JSON results.
accepted
The primary output of the Fast Query Recognizer, the accepted parameter returns 'true' if the input is believed to be an appropriate query for Wolfram|Alpha to process and 'false' otherwise.
timing
This parameter gives the CPU time (in milliseconds) used by the Recognizer to process the input.
domain
For accepted inputs (i.e. those that return 'true' for the accepted parameter), this parameter indicates the content domain under which the input is categorized. This gives a rough idea of the type of result you'd expect from sending this input to Wolfram|Alpha (either via the website or the other APIs).
resultsignificancescore
Using the Fast Query Recognizer API
Sample Query
Now that you have an AppID, you can make your first query. The base URL for queries is:
Every query requires three pieces of information—an AppID, a mode and an input value—in order to be processed correctly. The appid parameter tells your query which AppID to use:
The Fast Query Recognizer has two distinct modes, 'Default' and 'Voice', explained below. For the purposes of this sample query, we'll use the 'Default' mode:
Next, use the i parameter to specify the URL-encoded input for your query. For instance, here is a query for 'France':
When executed with a valid AppID, this URL will return an image with informational elements relating to the input:
URL Parameters and Options
You can add URL-encoded parameters to customize the behavior and output of the Fast Query Recognizer.
mode
The Fast Query Recognizer is available in two different modes, each of which is configured to accept certain types of inputs. 'Default' mode is designed to recognize any query for which Wolfram|Alpha returns a relevant result, with the goal of placing as many answers as possible into results. Some specific types of queries (e.g. phone numbers, IP addresses, product codes) are explicitly filtered, and only inputs with unambiguous linguistics are accepted (e.g. 'boston employment' is not accepted, but 'boston employment rate' is). This tuning up for ambiguity is an ongoing improvement.
The 'Voice' mode of the Fast Query Recognizer is optimized for spoken input. It is generally less restrictive than the 'Default' mode, meaning that more variation of the input will be accepted.
output
How To Type Subscript On Mac For Wolfram Alpha X
Results from the Fast Query Recognizer are available in both XML (default) and JSON formats using the output parameter. Here is the JSON version of the sample query and result from above:
How To Type Subscript Mac
Output Parameters
The following is an explanation of the output parameters given in XML and JSON results.
accepted
The primary output of the Fast Query Recognizer, the accepted parameter returns 'true' if the input is believed to be an appropriate query for Wolfram|Alpha to process and 'false' otherwise.
timing
This parameter gives the CPU time (in milliseconds) used by the Recognizer to process the input.
domain
For accepted inputs (i.e. those that return 'true' for the accepted parameter), this parameter indicates the content domain under which the input is categorized. This gives a rough idea of the type of result you'd expect from sending this input to Wolfram|Alpha (either via the website or the other APIs).
resultsignificancescore
This score is an initial estimate of how the Wolfram|Alpha result is expected to rank relative to search engine results, ranging from 100 (best) to 0 (worst, usually accompanied by a 'false' value for the accepted parameter). You can think of this as a measure of how certain Wolfram|Alpha is about a result, with higher scores indicating a higher degree of certainty.
summarybox
Shows the path to precomputed 'summary boxes' for the input, when appropriate.
Errors
HTTP Status 400
This status indicates that the API did not find an input parameter while parsing. In most cases, this can be fixed by checking that you have used the correct syntax for including the i parameter.
Invalid appid (Error 1)
This error is returned when a request contains an invalid option for the appid parameter. Double-check that you have entered an AppID and that your appid parameter is using the correct syntax.
Appid missing (Error 2)
This error is returned when a request does not contain any option for the appid parameter. Double-check that you have entered an AppID and that your appid parameter is using the correct syntax.
How To Type Subscript On Mac For Wolfram Alphabet
Permutations are among the most basic elements of discrete mathematics. They are used to represent discrete groups of transformations, and in particular play a key role in group theory, the mathematical study of symmetry. Permutations and groups are important in many aspects of life. We all live on a giant sphere (the Earth) whose rotations are described by the group SO(3) (the special orthogonal group in 3 dimensions). On the micro-scale, the Hungarian-American physicist Eugene Wigner (November 17, 1902â€'January 1, 1995), who received a share of the Nobel Prize in Physics in 1963, discovered the 'electron permutation group', one of many applications of permutation groups to quantum mechanics.
Ksn on kindle app for mac. Permutations deserve a full treatment in Wolfram|Alpha. Since Mathematica 8 provides new functionality to work with permutations using both list and cyclic representations, we now have a powerful new way of working with permutations using natural language.
Let's first define permutations, then discuss how to work with them in Wolfram|Alpha. A permutation of a set X is a bijective (one-to-one and onto) mapping of X to itself. There is a convenient way of specifying a permutation α of a finite set of n elements: write down the numbers 1, 2, …, n in a row and write down their images under α in a row beneath:
We call this two-line notation. For example, the permutation α of {1, 2, 3, 4, 5} with α(1)=3, α(2)=1, α(3)=5, α(4)=2, and α(5)=4 is written:
How To Type Subscript On Mac For Wolfram Alpha 1
Every permutation can be written as a cycle or as a product of disjoint cycles, for example in the above permutation {1 → 3, 3 → 5, 5 → 4, 4 → 2, 2 → 1}. One of the nicest things about a permutation is its cycle decomposition. Many times the most interesting information about a permutation are the lengths of its disjoint cycles. For instance, the following permutation decomposes into three cycles: one of length = 2 and two of length = 3.
Another common notation is a permutation list:
Wolfram|Alpha lists these different notations, typically in the first results pod.
We will now compute with permutations on a small set. (Why small? Say there are 100 elements in your set. Then there are 100! permutations, which would take you almost 3 x 10150 years to write if you wrote out one permutation every second.) Let's start by examining the properties of the permutation (1 2 5 3 7). Skyrim se horses for followers. As you can see, this permutation's notation pod has a button that toggles the display of fixed points, that is, the numbers that do not move.
A permutation is a bijection, which means that every permutation has an inverse function. Wolfram|Alpha computes a permutation's inverse and writes it in cycle notation. Then it gives the order of the permutation (when written in disjoint cycle form, the order is simply the least common multiple of the length of the cycles). After that is the index of a permutation α, which is the sum of all subscripts j such that α(j) >α(j + 1), 1 ≤ j< n. If you forget what these terms mean, there is a convenient Definitions button in the lower right corner of the pod, which opens a popup box displaying the definitions of the terms in the pod. Pressing the More button opens up a host of additional properties:
If you know which property you're looking for, just ask Wolfram|Alpha to return that property. For instance, the signature of a permutation is +1 if the number of transpositions (two element cycles) is even and -1 if it is odd. Let's find the signature or sign of the permutation list {4, 1, 5, 2, 3, 7, 8, 6}.
Now, function composition is a useful way to write permutations and is used specifically to study powers and products of permutations (note that the order in which you compose permutations matters), and for undergraduates learning about permutations for the first time, Wolfram|Alpha streamlines the learning process.
With products of permutations, the composition is assumed to be left to right.
Wolfram|Alpha provides a number of graphics to help us better understand permutations. One is the Permutation matrix, which Wolfram|Alpha displays both graphically and numerically:
The Cycle structure of the permutation nicely exhibits its action:
Wolfram|Alpha also knows about all kinds of special classes of permutations, such as involutions and derangements:
In combinatorics, it's often useful to construct all permutations. Usually the best way of doing this is in lexicographic order. Wolfram|Alpha understands this ordering and can rank and un-rank permutations lexicographically and give a mixed radix numbering for permutations using the factorial number system (also called factoradic).
Inversion is an important concept in the study of permutations. Inversions are pairs of elements that are out of order in the list form of a permutation. Inversions play a significant role in the analysis of sorting algorithms. One method of highlighting the inversions within a given permutation uses a so-called inversion graph (sometimes called a permutation graph). The inversion graph of a permutation α is a graph whose vertex set is {1, 2, 3, …, n} and whose edges {i, j} correspond exactly to (i, j) being an inversion in α. A clique in the graph corresponds to a decreasing sequence in the corresponding permutation.
Wolfram|Alpha also returns random permutations of any length:
Mathematica takes a unified approach to programming, so that new permutation functions seamlessly interact with all other Mathematica expressions. We illustrate this using Wolfram|Alpha:
There are plenty more applications and use-cases of permutations now in Wolfram|Alpha. Try them out and have fun with them. Also, be on the lookout for a permutation group blog post in the coming weeks!

